일단 간단한 문제로 시작해보자.
A B C 세 명의 사형수가 있다. 세 명 중 두명은 사형에 처하고 한 명은 무기징역으로 사면하겠다는 대통령의 결정에 따라 한 명은 무기징역을 받게 되었다.(무기징역이 사면인지 아닌지는 지금 이 문제의 논점과는 아무런 상관이 없다.) 대신, 공평하게 완전 랜덤으로 제비를 뽑아서 당첨된 사람이 무기징역을 받기로 했다. A B C는 번갈아 제비를 뽑았으나, 결과를 알지 못했다. 오직 정부만이 그 결과를 알고 있다. (이러한 상황이라고 해보자.)
어느 날 A가 "B, C 중 누가 죽는지 알아도 내가 사는지 죽는지 모르니 누가 죽는지 가르쳐달라."고 말했다. 이미 누가 죽는지 알고 있는 정부관계자는 "B가 죽는다."라고 말했다.
이 경우 B,C 중 죽는 사람이 최소한 한 명은 있고 한 명만(누가 죽는지) 말해준 것이기 때문에 확률에 영향을 미치지 않는다.(즉, A가 '오 B가 죽는구나. 그러니 이제 나랑 C 둘 중 하나만 죽는다고 봐도 되겠지? 내가 죽을 확률은 1/2이야'라고 생각을 해도 그게 틀렸다는 말이다.)그러므로, A의 입장에서 자신이 죽을 확률은 여전히 2/3이다.
그런데, 여기서 한 차원을 더해보자.
만약에 C도 정부관계자에게 단둘이 있을 때 물어보았고 같은 대답을 들었다면 확률이 어떻게 되는가?
("A,B중 누가 죽는지 알아도 내가 사는지 죽는지 모르니 누가 죽는지 가르쳐달라"라고 물었고 "B가 죽는다"라는 대답을 들었다면?) 그리고 A와 C는 그 후에 어떤 커뮤니케이션도 하지 않고 각자 방에서 기다리고 있다면?

결론만 말하자면, A의 입장에서는 자신이 죽을 확률이 2/3이 되고 상대방은 1/3이 된다. 역으로 C의 입장에서는 자신이 2/3이 되고 상대방이 죽을 확률은 1/3이 된다.
여기서 한 가지 가설을 세울 수 있는데, '똑같은 사건이어도 주체에 따라(관점에 따라) 확률이 달라진다' 다시 말해서, 확률은 상대적이라는 말이다!!
이 말이 왜 의미가 있을까?
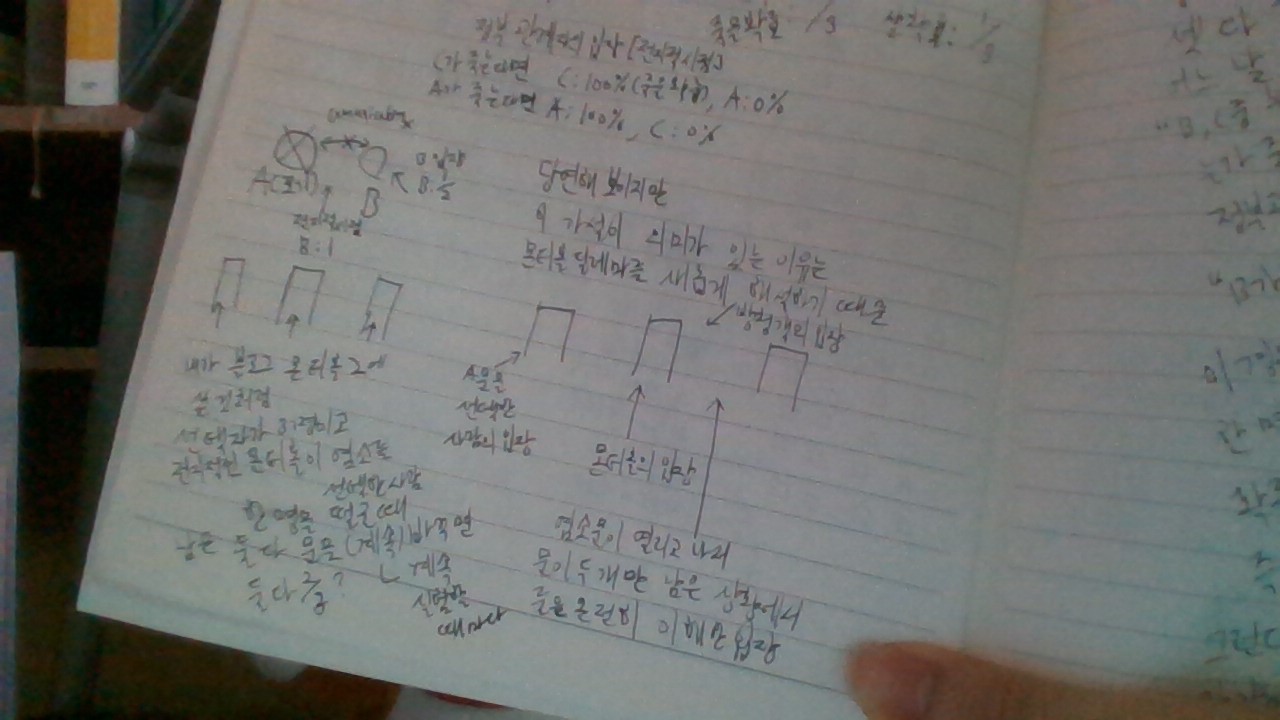
이 말이 의미가 있는 건 고전적인 딜레마를 해결해버리기 때문이다(몬티홀 딜레마) 몬티홀 기본 룰에 따르면, 맨 처음 문을 선택한 사람이 바꾸었을 때 포르쉐일 확률이 2/3임은 자명하다. 그런데 만약에 염소문이 열리고 나서 '하나의 문에는 염소가 있고 하나의 문에는 포르쉐가 있다는 걸' 이해한 사람이 있다고 해보자. (몬티홀 기본룰은 그대로 적용한다. 시점과 관점만 달라질 뿐이다.) 이 사람의 눈에는 아무리 눈씻고 보아도, 한 쪽이 1/2이고 반대쪽도 1/2이다. 이 사람에게는 이게 자명한 일이고, 그리고 그게 '옳은' 관점이다. 마지막으로 몬티홀 입장에서 생각해보자. 이 사람은 어디에 포르쉐가 있는지, 어디에 염소가 있는지 다 알고 있다. 이 사람은 한 쪽은 1이고 한 쪽은 0이다.(확률적 관점) 맨 처음 문을 선택한 입장, 염소문이 열리고 나서 문이 두 개만 남은 상황에서 본 방청객 입장, 몬티홀 입장 등등 '똑같은 사건이어도 확률은 각기 다르다' 그리고 이는 자명한 일이다. 이렇게 몬티홀 딜레마는 풀린다.
몬티홀 딜레마가 그동안 딜레마였던 이유는 이렇게 각자의 입장이 다르다는 걸 깨닫지 못하고 수학교수랑 똑똑이랑 논쟁이 붙었기 때문이다. 가장 정확한 답은 그 모든 관점에서 본 각자의 확률 판단이 모두 맞다는 것이다. 한 마디로 확률은 상대적이다.
'수학(Curiosity)' 카테고리의 다른 글
| 솔로몬의 판결 (0) | 2021.04.08 |
|---|---|
| 흥미로운 질문 (0) | 2021.04.08 |
| 수학의 얼굴 (0) | 2019.03.07 |
| 수학과 논리적인 사고 (0) | 2019.02.24 |
| 무한 (0) | 2019.02.01 |